Today we're going to look at legs and the way that they move. This is in service of a larger project that may or may not pan out, but I think the system I came up with is pretty interesting and quite unlike any existing procedural animation techniques I've seen.
What is a leg even really?
Long ago the only things that had bones were fish. And then some of those fish got nuts and decided to get out of the water. One thing led to another and now all sorts of bony leg-having creatures dominate the earth, and we call these things tetrapods. There are also arthropods which have a different kind of bone-less leg, but we're going to ignore them for now.
Tetrapods are cool because if you compare the limb bones across different species, you will find that they are structurally very similar because they all descend from the same nubby proto-legs that those ancient fish developed.
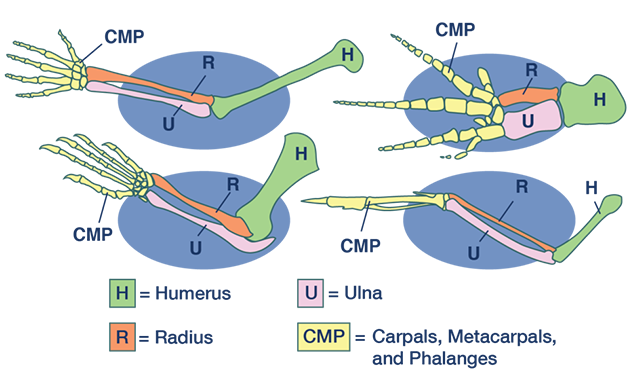
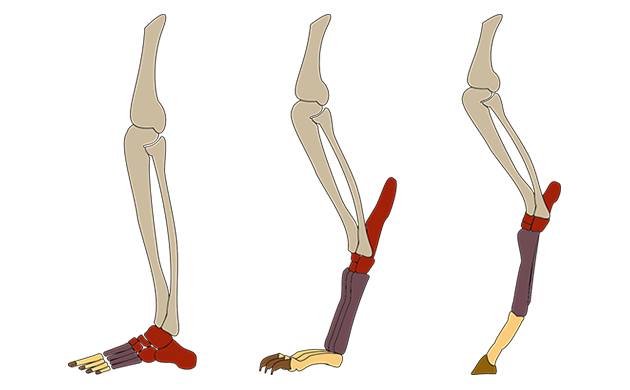
Limbs can do all sorts of crazy things, but today we're just concerned with walking, so we're going to be specifically modelling some tetrapod legs. These legs generally fall into three categories:
- plantigrade legs, where the metatarsals lie flat along the ground (e.g. human legs)
- digitigrade legs, where toes rest on the ground but the ankle is lifted up (e.g. cat legs)
- unguligrade legs, where the whole "foot" is lifted up almost vertically and the animal walks on what are effectively its toenails (e.g. horse legs)
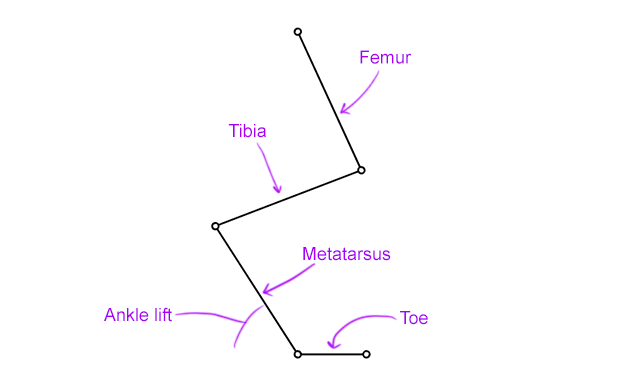
Since these three types of leg are made from the same parts and sort of blend into one another, I wanted to develop one single parametric "meta-leg" which could be configured to represent each of these.
To accomplish this, our creature's legs will have four bones/segments: femur, tibia, metatarsus, and toe (for simplicity I'm going to use these names for both front and back legs). The parameters for a leg will include the lengths of these segments, as well as an "ankle lift" factor which determines the angle between the metatarsus and the ground when standing. Toes will always lie flat on the ground, and we can cheat a bit to get unguligrade legs by just reducing the toe length to zero.
Implementing legs
Normally, a 3D character model in a game or animation software is accompanied by a bunch of bones that let you contort the mesh.
In practice, there are some bones (like the ones making up an arm or leg) that you, as the animator, don't always want to move one-by-one. It's often more convenient to just put the hand or foot wherever you want it to be, and then have the rest of the arm or leg figure out how it needs to bend to make that work. This process where a limb "figures out" how to pose itself is called inverse kinematics (IK).
To make something walk or run, we also only really care about how its feet move, and so our legs will be completely driven by inverse kinematics. Let's start with a simple example.
A quick primer on IK
The simplest practical example for understanding IK is a 2-link kinematic chain (e.g. a leg with one bone between the hip and knee, and another between the knee and foot). If we know the position of the hip and the position of the foot, we can use some trigonometry and analytically determine the angle and position of the knee.
I was going to make a little demo of this on Desmos but I found one that someone else made and it's a lot nicer than what I probably would've done. So shout-out to whoever made this: https://www.desmos.com/calculator/zds5lmt401
Here's the gist: the hip, foot, and knee form an imaginary triangle, and it turns out that we know all three side lengths of this triangle. So using the law of cosines and some other trig you probably learned in high school, we can find the internal angles of the triangle and its rotation in space, and from there we can find the position of the knee joint.
This is obviously very cool and exciting, but our creatures' legs will have more than two segments. You might think we can sneak in an extra link or two and keep solving everything analytically. Well guess what, we can't! At least not without getting creative. It turns out that when you add more degrees of freedom, the system becomes redundant and underconstrained meaning there are infinitely many solutions and our analytical approach no longer works. I don't want to get into this too deeply here, but there are other good resources you can check out if you want to really get into the math behind IK.
Of course there are ways to solve these types of redundant systems. General purpose IK solvers usually employ some kind of numerical method that figures out the chain's pose using gradient descent or Netwon's method. These work pretty well, and we will need to go this route eventually if we end up implementing body parts like necks and tails, but numerical methods tend to be more computationally expensive and offer less precise control. It would be better to stay in the nice clean world of analytical solutions for as long as possible. And fortunately for us, that is still an option. All we have to do is get a little creative.
Getting a little creative
The key to getting back to an analytical solution is eliminating the redundancy of our kinematic chain, meaning the "extra" joints are fixed or determined some other way. Then we can run IK on the rest of the leg, which is no longer underconstrained. There's no one "correct" way to do this, so we're kind of just winging it and getting the leg's movements to look good.
First of all, I think we can safely ignore the toe bone in our actual kinematic chain. It makes more sense for our "end effector" to be the joint between the metatarsus and the toe because that's what we want making contact with the ground. The toe kind of just sticks out from there and it will move with the rest of the foot (we can always animate it later). So our actual kinematic chain is three links: femur, tibia, and metatarsus.
Since we decided that our "ankle lift" parameter would determine the angle between the metatarsus and the ground, we can start by fixing the orientation of the metatarsal bone. All we have to do is take the ankle lift and use some trig to find the x and y coordinate offset of the ankle joint from the foot target. And once we know our ankle position, we've reduced the IK problem back down to two links, meaning it's solvable!
Obviously this isn't looking great. The metatarsus is not rotating at all no matter how the rest of the leg moves. Let's at least have it inherit the rotation of the entire leg. We'll find the angle between the y-axis and the straight line from the hip to the foot. Then we can add this angle to the ankle lift before positioning the ankle joint. We'll also use this angle to rotate the toe.
Now we're cooking. I also want the ankle to bend in and out as the leg flexes and extends. To do this, I'm going to add another parameter to our leg that I'm calling the "natural bend". We can figure out the maximum length of the leg at full extension, and the natural bend says what percentage of this is the leg's neutral resting length. Then, if the distance from the hip to the foot is shorter or longer than this, the effective ankle lift decreases or increases accordingly.
This one is a little more subtle, but it particularly helps when the leg extends towards its maximum length. There are still some edge cases where this looks kind of wonky, and you could certainly come up with some clever ways to make it look even better, but I'm happy enough with it to leave it as is.
Here's the fully functional leg on Desmos.
I implemented this in Godot and put a dummy creature together with four of these legs. The front legs work the same way as the back, but the knee joint bends in the opposite direction. Also I made the toes lie flat whenever the foot was touching the ground, so that they look a little more realistic.

Now let's put those legs to use.
Gait
A leg's main function is locomotion, and the particular way an animal moves it's legs as it locomotes is called a gait. Animals use different kinds gaits for all sorts of reasons, but movement speed tends to be the main one (a dog's feet move very differently between a walk and a run).
Each gait is a cyclical pattern within which each leg completes a full step — a step being composed of an airborne "swing" phase and a grounded "stance" phase.
The two most distinguishing factors of a gait are:
- The phase differences between each foot
- The relative duration of the swing and stance portions of the step (sometimes called the duty factor).
We'll be controlling the movement of our dummy's feet using oscillators that effectively break down into two periodic waves: one driving the front-back motion of the foot and the other (offset by a \(\frac{\pi}{2}\) phase shift) driving the up-down motion. For now these will just be plain sine waves. Let's take a look.
Wow, look at him go! This is obviously not a very realistic gait — all of the legs are synchronized with each other. Let's fix that.
Leg phase differences
This part is pretty straight forward. All we have to do is give some of the foot oscillators a phase shift so that they don't all step at the same time. We could set each one individually, but I prefer to generate the four offsets from a combination of two variables that we control: one phase offset between the front and back legs and another between the left and right legs. These are additive so the difference between the front-left leg and rear-right leg is the sum of these two values.
Let's start by setting a phase offset of \(\pi\) between the left and right foot oscillators.
Now we're getting somewhere! This is a type of gait called a pace (although a pace is usually faster than this). Let's add some offset between the front and back legs now. Something around \(\frac{\pi}{2}\) should give us something that resembles a normal walk.
This is already starting to look pretty good in my opinion. We can get all sorts of very different looking gaits if we just mess around with these two phase offset values.
Swing-stance ratio
A step cycle is always split into a part where the foot is planted on the ground (the stance phase), and a part where the foot is in the air (the swing phase). So far in our creature's gaits, these have been equal in proportions. But in real life, faster gaits have shorter stance phases and longer swing phases, and slower gaits have the inverse. If we want to our gait animations to look more convincing, we can't just speed up or slow down the whole animation: we need a way to manipulate our oscillators' swing-stance ratio.
Let's first consider the sine wave driving the up-down motion of the foot. Clearly, if we want to bias towards a longer swing phase we will need to squash the part of this wave that is below zero and proportionally stretch out the part above zero (and vice versa for biasing in the other direction). There are probably a few good ways to accomplish this, but after fiddling around in Desmos for a while I came up with this mess of a function to replace our plain sine wave:
$$ f\left(x,k\right)=2\frac{k^{\sin\left(x\right)}-\frac{1}{k}}{\left(k-\frac{1}{k}\right)}-1 $$
\(x\) is the time input like before, and \(k\) is the "skew factor" whose range is \((0, \infty)\)
When \(k\) is very small, the wave becomes dominated by the positive part, and when \(k\) is very large, it becomes dominated by the negative part. You can play around with this yourself here.
At \(k=1\) this function is actually undefined, but the wave function starts to become a normal sine wave as \(k\) approaches \(1\) from either side, so we can just handle that as an edge case in our implementation.
So now our foot can spend more time on the ground or in the air, but the front-back movement no longer syncs up with the up-down movement. The foot oscillator's other wave function needs to be modified as well.
The foot should ideally be moving forward throughout the swing phase and backward throughout the stance phase. If the foot is in the air for a shorter time than it is on the ground, it will have to move forward faster than it moves backwards, meaning we have to squeeze the rising slope of the wave, and stretch the falling slope.
Again I fiddled around in Desmos until I came up with a function that did roughly what I was looking for. Here it is:
$$ f\left(x,k\right)=\frac{1}{k}\arctan\left(\frac{k\sin\left(x\right)}{1-k\cos\left(x\right)}\right) $$
Here the skew factor \(k\)'s range is \((-1, 1)\), and effectively becomes a sawtooth wave at the extremes. This is also undefined at \(k=0\), but just like our other function, it approaches a normal sine wave as \(k\) gets close to zero, so we can handle this edge case the same way. You can play around with this function here.
The final piece in this puzzle is matching up the two skew factors for the waves. This was a little trickier than I wanted it to be. You ideally want the x-intercepts of one wave to perfectly line up with the stationary points of the other wave, across all valid skew factors. I wasn't quite able to do that, but I got close enough to have it look good in practice. We'll take a bias factor \(b\) and use it to generate our skew factors as follows:
$$ k_{duty} = e^b $$
$$ k_{slope} = \frac{2}{\pi}\arctan\left(b\right) $$
\(b\) can be any real number, and skews both waves symmetrically for positive and negative values. I made another Desmos graph that that overlays the two waves here.
Now that we figured that out, we can upgrade our foot oscillator to use these functions instead of normal sine waves, and we can have "swing-stance bias" be another parameter we can put in our gait-making toolbox:
We can bias towards the swing phase for fast gaits like a gallop:
and we can bias towards the stance phase for slow gaits like a walk:
Final touches: body movement
At this point, the most important parts of the gait animation are done, but it's still looking pretty stiff. Naturally you would expect the body itself to be a little more dynamic when the legs are moving all over the place, so let's make that happen. This write-up is already longer than it deserves to be, though, so I'm going to be super brief here.
As you can probably see, our creature's body is made up of a bunch of segments, and the legs are attached to the ones at the very front and back. Let's have these first and last segments bob up and down throughout the walk cycle. You could probably do this with some kind of pseudo-physics simulation, but I just sample the two foot oscillators with a bit of offset, and use those values to set the height of the body segment and I think it looks pretty good.
We can also make the body segment turn left and right very slightly depending on which foot is forward and how far apart the left and right feet are.
Then after setting the position and orientation of these two body segments I generate a cubic Bezier curve between them and place the rest of the body segments along this curve. This is a quick and dirty way to make the body look like it has a spine that is twisting and bending as the creature moves.
Wrapping up for now
That pretty much covers everything I've done so far. I've got more ideas that I want to incorporate, but I'm trying to get better at finishing one thing at a time so that I can document my progress with these write-ups.
The next thing I'd like to tinker with is combining our current gait animation with a more "traditional" kind of procedural walk animation, where the foot stays planted at some position while the body moves forward in space, and then quickly steps forward when the body gets too far away. Currently our creature is kind of just moonwalking in place, but we obviously want him to be able to move around in some environment. We could slide the whole creature forward as he's walking, but this starts to look really bad if the movement speed and animation aren't perfectly synced up. And what if the ground is uneven or he's going up a flight of stairs?
Also tetrapods obviously aren't the only animals with legs. There are all sorts of arthropods like bugs and crabs that have different kinds of legs. And legs aren't even the only type of limb! How would we implement wings, arms, and flippers?
Anyway, you can check out the source code of the final Godot project here.
(I'll try to get a web build of this up and running soon)